1. Propiedades de una sumatoria
Número de términos en un sumatorio
Dada la suma: 
Donde el número de términos siempre es igual al número resultante de reemplazar y realizar la siguiente operación: ![]() . En otras palabras, si el límite inferior es positivo, el número de términos de un sumatorio va a ser igual al límite superior menos el límite inferior más uno. Comprobémoslo en los siguientes ejercicios.
. En otras palabras, si el límite inferior es positivo, el número de términos de un sumatorio va a ser igual al límite superior menos el límite inferior más uno. Comprobémoslo en los siguientes ejercicios.
Halle el número de términos resultante, al desarrollar las siguientes sumatorias:

Solución:
![]()
Al desarrollarla se obtendría:
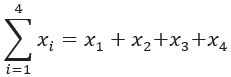
Obteniendo así 4 términos. Esto también lo podríamos haber obtenido al realizar:
![]()
Comprobamos reemplazando los valores del ejercicio:
![]() términos.
términos.
![]()
Al desarrollarla se obtendría:
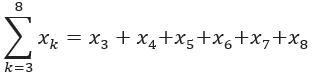
Obteniendo así 6 términos. Esto también lo podríamos haber obtenido al realizar:
![]()
Comprobamos reemplazando los valores del ejercicio:
![]() Términos.
Términos.
Nótese que solo hemos calculado el número de términos, no hemos resuelto la sumatoria como tal, ya que no teníamos los valores de cada término.
2. Principales propiedades de los sumatorios, aplicadas en la gestión
A continuación, veremos las propiedades más utilizadas en carreras de gestión empresarial tales como: administración de empresas, contabilidad y finanzas, ingeniería industrial, ingeniería empresarial o ingeniería comercial. Si requieres una propiedad que no está acá, te recomendamos revisar textos matemáticos relacionados a “sucesiones, inducción y sumatorias”.
Nota: El sumatorio, al ser simplemente el resumen de una suma, cumple con todas las propiedades de una suma
a) sumatoria de una constante
![]() es una constante real que no depende de i
es una constante real que no depende de i
Expresado de manera verbal:
La sumatoria de una constante que no depende del subíndice, es la multiplicación de la constante cuantas veces indique la sumatoria.
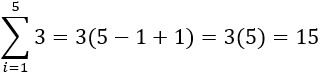
Comprobando:
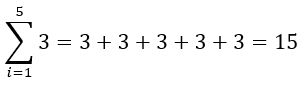
b) propiedad conmutativa
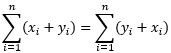
Expresado de manera verbal:
Propiedad conmutativa, al cambiar el orden de los términos, permanece el mismo resultado.
Ejemplo de la propiedad conmutativa aplicada en un sumatorio
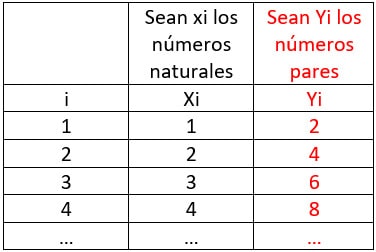
Nota: Se ha pintado de rojo para su fácil seguimiento durante el desarrollo.
Comprobar que:![]()
Primero hallaremos el resultado de: ![]()
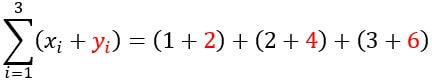

Ahora hallaremos el resultado de: ![]()
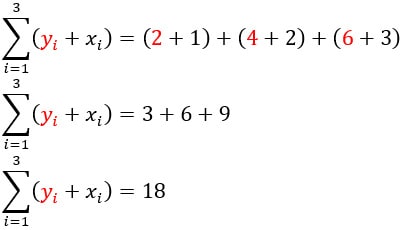
Como ambos valores son iguales a 18, queda comprobado que:
![]()
![]()
Expresado de manera verbal:
Propiedad distributiva, el valor de una sumatoria donde existe una constante multiplicada por los sumandos, es el mismo que el valor que se obtiene al multiplicar la constante por la sumatoria.
c) propiedad distributiva

Expresado de manera verbal:
Propiedad distributiva, el valor de una sumatoria donde existe una constante multiplicada por los sumandos, es el mismo que el valor que se obtiene al multiplicar la constante por la sumatoria.
Ejemplo de la propiedad distributiva aplicada en un sumatorio:
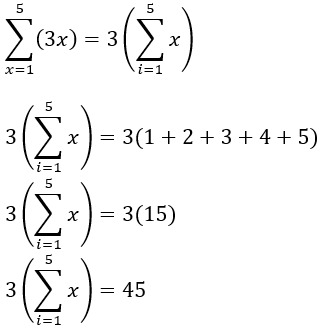
Comprobando:
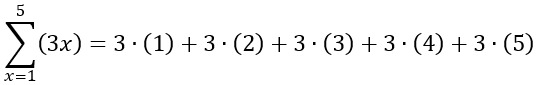
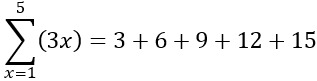
![]()
d) propiedad asociativa
![]()
Expresado de manera verbal: Propiedad asociativa, el resultado de una suma es siempre el mismo sin importar cómo agrupemos los términos. En este caso, la sumatoria de una suma, es igual a la suma de las sumatorias individuales.
Ejemplo de la propiedad asociativa aplicada en un sumatorio
Nota: Se ha pintado de rojo para su fácil seguimiento durante el desarrollo.
Hallar: ![]()

Comprobando:

e) La sumatoria partida en una diferencia de sumatorias
La sumatoria partida en una diferencia de sumatorias, cuando inicia en un término diferente al primero
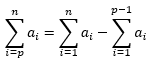
Expresado de manera verbal: La sumatoria desde el término “p” hasta el término “n”, es igual a la sumatoria desde el término 1 hasta el término “n” menos la sumatoria desde el término 1 hasta el término “p-1”.
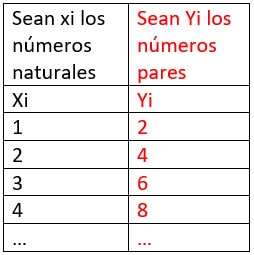
Ejemplo de una sumatoria partida en una diferencia de sumatorias:
Sean los valores pares:
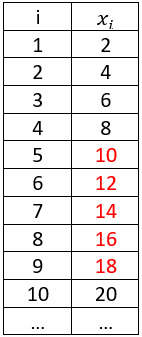
Comprobar que: ![]()
Primero hallaremos el resultado de: ![]()

Ahora hallaremos el resultado de: ![]()

Ahora hallaremos el resultado de: ![]()

Ahora hallaremos el resultado de:
![]()

Como ambos valores son iguales a 70, queda comprobado que:
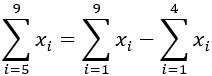
Sumatoria notable
Una sumatoria notable es aquella que, si cumple con ciertas características, tiene una manera corta de calcular. La más utilizada es la que nos ayuda a sumar los primeros números naturales, es decir que la sumatoria empieza desde el uno y lo sumandos son los números naturales consecutivos. Si se cumplen estas condiciones, entonces se la puede calcular mediante la siguiente fórmula:

Expresado de forma verbal: la sumatoria de los primeros números consecutivos naturales, es decir que se suma desde el 1, 1 a 1, hasta el número “n”, es igual a la multiplicación del número “n” por el siguiente número consecutivo a “n”, dividido entre dos.
Demostración de la sumatoria notable de los primeros números naturales.
Demostrar que:
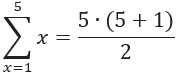
Primero calculamos: ![]()

Ahora calculamos: ![]()
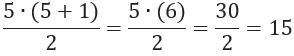
Como ambos valores son iguales a 15, queda comprobado que:

Ejercicios de sumatorias, resueltos aplicando propiedades
¡Ahora te toca a ti!
Resuelve los siguientes ejercicios, y comprueba tus respuestas con el video que aparece al final.
I Calcular el valor de las siguientes sumatorias:

II Plantea y calcula las siguientes sumatorias:
a. Calcule la suma de todos los números pares desde 1 hasta 30
b. Calcule la suma de todos los números impares desde 1hasta 25
Comprueba tus resultados
con el siguiente video:








Cuáles son los elementos dela sumatoria
Hola Heydi,
Muchas gracias por tu consulta, a continuación mi respuesta:
Los elementos principales de una sumatoria son:
Símbolo sigma (Σ): Esta letra griega mayúscula es la que representa la operación de suma.
Índice de suma (i): Es una variable que toma valores enteros consecutivos dentro de un cierto rango. Este índice indica qué término de la secuencia se está sumando en cada paso.
Límite inferior (a): Indica el primer valor que toma el índice de suma.
Límite superior (b): Indica el último valor que toma el índice de suma.
Término general (a_i): Es una expresión matemática que depende del índice de suma y determina el valor de cada término de la secuencia.
Saludos y éxitos!
Marco Villena