Permutaciones con repetición
¿Cuántas ordenaciones distintas se pueden formar con las letras de la palabra POMABAMBA?
Imagine que coloca las 9 letras de POMABAMBA una tras otra en 9 lugares:

Para resolver este tipo de ejercicios, analizaremos las permutaciones con repetición, también llamadas permutaciones con conjuntos de objetos no distinguibles. Antes de entrar a analizarlo, se deben recordar algunos conceptos:
El factorial de un número
Está dado por:
![]()
Conteo de subconjuntos de un conjunto: combinaciones
Sean n y k enteros no negativos con k ≤ n. Una k-combinación de un conjunto de n elementos es un subconjunto de k de los n elementos. El símbolo (n,k), que se lee “de n elija k”, denota el número de subconjuntos de tamaño k (k-combinaciones) que se puede elegir de un conjunto de n elementos.
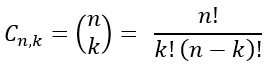
Permutaciones con repetición
Si al formar grupos con los n elementos de un conjunto, se repiten algunos de ellos, se trata de una permutación lineal con repetición.
De n elementos distintos, donde α, β, θ… indican la cantidad de elementos repetidos, son los diferentes grupos que pueden formarse con los n elementos dados, de modo que dos grupos difieren entre sí porque sus elementos están en distinto orden. Entonces el número de permutaciones de los n objetos es:
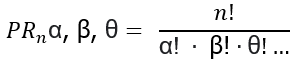
¿Cuántas ordenaciones distintas se pueden formar con las letras de la palabra ARITMÉTICA?
1. ¿Cuántos espacios hay?
n=10
2. ¿Cuántos elementos repetidos hay?
Elementos repetidos = 3
3. ¿Cuántas veces se repite cada elemento?
A = 2 I = 2 T = 2
4. ¿Cuántas ordenaciones distintas se pueden formar?
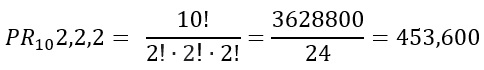
Comprueba tus resultados
con el siguiente video:
EJERCICIOS DE
PERMUTACIÓN CON REPETECIÓN
a





Deja tu comentario